A MACRODISPERSION MODEL FOR PLUME MIGRATION IN WEAKLY HETEROGENEOUS MEDIA (ln K VARIANCE 0.5) WITH PORE-SCALE DISPERSION  
Parameters & Legend | Problem Statement | Key Observations | Additional Observations | Mathematical Interpretation
Parameter Case 1 Case 2
Geometric mean hydraulic conductivity, Kg (m/day) 10 10
ln K variance 0.5 0.0
Correlation scale, λ (m) 1 NA
Porosity, n 0.3 0.3
Longitudinal pore-scale dispersivity (m) 0.01 NA
Transverse pore-scale dispersivity (m) 0.001 NA
Longitudinal macrodispersivity (m) NA 0.5
Transverse macrodispersivity (m) NA 0.0008125
Head difference (m) 1 1
Size of model (m) 200 x 50 200 x 50
Covariance function Exponential Exponential
Approximate initial plume size (m) 10 10
Grid 801 x 201 801 x 201
Cell size, Δx (m) 0.25 x 0.25 0.25 x 0.25
Time step, Δt(days) 1 1

The model parameters and inputs are explained below:

  • The ln K field is a normally distributed random field. Therefore, there is an equal probability of the plume encountering a ‘low' K zone or a ‘high' K zone.
  • The heterogeneous conductivity field is uniquely characterized by the following set of statistical parameters: geometric mean ( Kg) of K , correlation scale, variance and covariance.
  • The geometric mean, ln K variance and correlation scale are constant for both cases.
  • The covariance function for both cases is exponential.
  • Case 1 has longitudinal and transverse dispersivities of 0.01 m and 0.001 m respectively, while they do not apply to case 2. The corresponding macrodispersivities for case 2 are 0.5 m and 0.0008125 m.
  • The cell size, Δx, is selected such that the correlation scale, λ, is resolved. Typically, Δx is at least 3 to 4 times smaller than the correlation scale.
  • The time step, Δt, is selected such that a particle of the plume travels a distance that is less than λ in one time step.

Download model - 1 (To download, right click and select "Save Link As" )

Download model - 2

A MACRODISPERSION MODEL FOR PLUME MIGRATION IN WEAKLY HETEROGENEOUS MEDIA (ln K VARIANCE 0.5) WITH PORE-SCALE DISPERSION
 Problem Statement

This video compares two different modeling techniques to predict macrodispersion of a conservative solute plume in a weakly heterogeneous medium. The first technique employs a detailed description of spatial variability of conductivity using statistical parameters, and a pore-scale dispersion coefficient. The second technique uses Gelhar's asymptotic macrodispersion model ( Gelhar and Axness, 1983a ) that consists of a homogeneous medium and a macrodispersion coefficient. This video demonstrates the effectiveness of Gelhar's model in predicting plume spreading. The modeling domain consists of constant head boundaries on the left and right extremes, and no-flow boundaries at the top and bottom; the initial size of the plume is significantly larger than the correlation scale of heterogeneity. Details are provided in Table 3.1.

 Key Observations

The following observations can be made from the video:

  • The macrodispersion model approximately predicts plume location and amount of spreading in both longitudinal and transverse directions.
  • The macrodispersion model is unable to predict the irregular shape of the plume, and hence, the maximum concentration and degree of dilution.

Similar experiments with larger perturbations (higher ln K variance) are shown in subsequent videos.

 Additional Observations

Gelhar's macrodispersion model attempts to predict the large-scale spreading that occurs in a heterogeneous field. The underlying assumption for the macrodispersion model is that the conductivity perturbations in the heterogeneous field are small. These perturbations control plume spreading in the heterogeneous field. Longitudinal spreading in the heterogeneous field is greater than transverse spreading. The macrodispersion model predicts that the longitudinal spreading is directly proportional to the correlation scale of heterogeneity and the ln K variance, and transverse spreading is directly proportional to the pore-scale dispersivity and the ln K variance. Since the correlation scale is at least two orders of magnitudes larger than pore-scale dispersivity, longitudinal spreading is significantly larger than its transverse counterpart. Therefore, the macrodispersion model is able to predict the overall spreading of the plume approximately.

Since the macrodisperion model consists of a homogeneous medium, the plume obtained is always regular. As a result, the irregular shape of the plume seen in the heterogeneous field is not predicted. The irregular shape of the plume translates to irregular variations of concentration, which are also not predicted. Consequently, the macrodispersion model is unable to accurately predict the maximum concentration and the degree of dilution of the plume.

* Mathematical Interpretation

The following equations show the relationship between pore-scale dispersion and macrodispersion:

,
(3.1.1)

,
(3.1.2)
where: C = Concentration; ui = Seepage velocity; Dij= Dispersion coefficient.

It can be shown [ Gelhar and Axness, 1983a ] that:

.
(3.1.3a)

The coefficient Aiiis called macrodispersivity and is given by [ Gelhar, 1993 ]:

,
(3.1.3b)

where: = ln K variance; λ = Correlation scale; A11 = Longitudinal macrodispersivity; A22 = Transverse macrodispersivity; αL= Longitudinal dispersivity; αT= Transverse dispersivity.

Equation (3.1.3b) shows that the longitudinal macrodispersion is unaffected by pore-scale dispersion, whereas transverse macrodispersion is affected. Therefore, the magnitude of longitudinal macrodispersion is many orders of magnitude larger than the transverse macrodispersion. Substituting (3.1.3a) into (3.1.2):

,

(3.1.4)

.

(3.1.5)

The pore-scale dispersivity, αij, is typically one-hundredth of a meter, while the macrodispersivity, Aij , is approximately one meter. Therefore, macrodispersion is the dominant process and controls the total spreading of the plume.

Equation (3.1.5) simplifies the complex heterogeneous field, represented by (3.1.2). A simple mean macrodispersion model is obtained by replacing the dispersion coefficient with a macrodispersivity value. This model can predict the mean spreading of the plume.
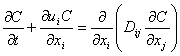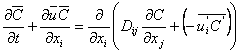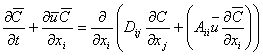