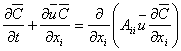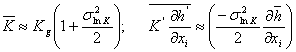EFFECTS OF HETEROGENEITY OF HYDRAULIC CONDUCTIVITY
Parameters & Legend | Problem Statement | Key Observations | Additional Observations | Mathematical Interpretation
Parameter Case 1 Case 2 Case 3 Case 4
Geometric mean hydraulic conductivity, Kg (m/day) 10 10 10 10
ln K variance 0 0.5 1.0 3.0
Correlation scale, λ (m) NA 2 2 2
Porosity, n 0.3 0.3 0.3 0.3
Local pore-scale dispersivity 0 0 0 0
Head difference (m) 1 1 1 1
Size of model (m) 200 x 50 200 x 50 200 x 50 200 x 50
Covariance function NA Exponential Exponential Exponential
Approximate initial plume size (m) 10 10 10 10
Grid 401 x 407 401 x 407 401 x 407 401 x 407
Cell size, Δx (m) 0.5 x 0.5 0.5 x 0.5 0.5 x 0.5 0.5 x 0.5
Time step, Δt(days) 1 1 1 1

The model parameters and inputs are explained below:

  • The ln K field is a normally distributed random field. Therefore, there is an equal probability of the plume encountering a 'low' K zone or a 'high' K zone.
  • The heterogeneous conductivity field is uniquely characterized by the following set of statistical parameters: geometric mean (Kg) of K, correlation scale, variance and covariance.
  • The mean is constant for all cases, while the ln K variance increases from 0 to 3.
  • The correlation scale does not apply to case 1 and is a constant for cases 2, 3 and 4.
  • The covariance function for cases 2, 3 and 4 is exponential.
  • The cell size, Δx, is selected such that the correlation scale, λ, is resolved; typically, Δx is at least 3 to 4 times smaller than the correlation scale.
  • The time step, Δt, is selected such that a particle of the plume travels a distance that is less than λ in one time step.

EFFECTS OF HETEROGENEITY OF HYDRAULIC CONDUCTIVITY
 Problem Statement

This video demonstrates the effect of heterogeneous hydraulic conductivity media on the transport of a conservative solute in the absence of pore-scale dispersion. The initial size of the plume is much larger than the scale of heterogeneity. The modeling domain consists of constant head boundaries on the left and right extremes, and no-flow boundaries at the top and bottom. Case 1 has a homogeneous field; and cases 2 through 4 show increasing degrees of heterogeneity. Details are provided in Table 1.1
 Key Observations

The following observations can be made from the video:

  • Although there is no pore-scale dispersion, the plume spreads because of heterogeneity. This large-scale spreading is called macrodispersion.
  • As long as the plume encounters heterogeneity, it continues to spread.
  • Plume spreading increases with increasing ln K variance.
  • Longitudinal spreading is significantly greater than transverse spreading.
  • Mean displacement remains largely unaffected, despite the heterogeneity.
  • Transport through heterogeneous media results in complex irregular plumes; in homogeneous media the plume remains regular.
 Additional Observations

The pattern of plume spreading shows a clear trend. The plume does not spread at all when the ln K variance is 0.0, and spreads the most when the ln K variance is 3.0. Even though the plume spreading is enhanced, the mean plume displacement is largely unaffected. The fingers of the plume contain the maximum mass of the plume, but are concentrated over a small spatial area. The tails have less mass, but are elongated. Consequently, the center of mass, and thus mean displacement, remains the same, irrespective of the ln K variance.

The effect of the symmetric ln K field on plume spreading is asymmetric. The fingers (leading edge) of the plume are shorter than the tails (trailing edge) of the plume, which results in a skewed plume. This can be explained very simply. High K zones are convergent zones, through which the plume prefers to travel, and in which it converges. Convergence is the opposite of spreading. Therefore, shorter fingers are found. In contrast, low K zones are zones of divergence, which impede the movement of the plume. When a low K zone is encountered, the plume travels around it rather than through it and this results in spreading. If a part of the plume reaches the low K zones, it gets 'trapped' due to the extremely low velocities in that zone. The bulk of the plume continues moving, while the portion trapped in the low K zone is released slowly; thus contributing to tail elongation.
* Mathematical Interpretation

Mathematically, these processes can be explained using the following equations. In a heterogeneous field, in the absence of pore-scale dispersion, the conservative solute concentration at any point for any irregular plume realization is given by:

,

(1.1.1)

where: C = Concentration; ui = Seepage velocity.

To determine large scale behavior, the method of perturbation is used, and on performing local spatial averaging, we get the following:

,

(1.1.2)

where: = Mean concentration; = Perturbation to mean concentration; = Mean seepage velocity; = Perturbation to mean seepage velocity.

This additional term on the RHS of (1.1.2) reflects the effects of heterogeneity.

It can be shown [ Gelhar and Axness, 1983a ] that:

.

(1.1.3a)

The coefficient Aiiis called macrodispersivity and is given by [ Gelhar, 1993 ]:

,

(1.1.3b)

where: = ln K variance; λ = Correlation scale; A11 = Longitudinal macrodispersivity; A22 = Transverse macrodispersivity; αL= Longitudinal pore-scale dispersivity; αT= Transverse pore-scale dispersivity.

Substituting (1.1.3a) into (1.1.2), yields:

.

(1.1.4)

This is the classical advection-dispersion equation. The additional term on the RHS in (1.1.4) represents macrodispersion. From (1.1.3b), it is evident that with increasing ln K variance, the longitudinal component of macrodispersion will increase. However, there will be no effect on transverse macrodispersion, since no pore-scale dispersion is present.

The mean velocity ( ) controls the mean displacement of the plume. Darcy's equation gives the seepage velocity of the flow as:

,

where: K = Mean conductivity; n = Porosity.

The mean velocity is given by:

.
(1.1.5)

Gelhar ( 1993, equation 4.1.48 ) showed that

,

(1.1.6)

where: K ' = Perturbation to mean conductivity; = Mean hydraulic head; = Perturbation to mean hydraulic head; Kg= Geometric mean of hydraulic conductivity.

Substituting (1.1.6) into (1.1.5), we get:

.

(1.1.7)

Since the geometric mean hydraulic conductivity and mean hydraulic gradient are the same for all cases, is the same. As a result, the mean plume displacement remains largely unaffected.